GPT-5 Pro独立攻克数学未解区间：AI展现前沿问题解决新突破

微软前AI副总裁兼杰出科学家Sebastien Bubeck发表文章称，GPT-5 Pro成功从零开始攻克了数学论文中的一个未解区间，这一突破性发现令他深感震撼。该成果引发了众多领域专家的转发讨论，OpenAI总裁Greg Brockman认为人工智能或将显著加速数学研究进程。

人工智能是否真能解决人类面临的前沿难题？

例如像庞加莱猜想、麦克斯韦方程求解、费马大定理、黎曼猜想等历史性难题。

如今，这个问题似乎找到了肯定的答案。

AI确实具备了这种潜力！它完全独立运作，未借鉴人类已有的任何方法。

近期，GPT-5 Pro展示了从零开始完全求解复杂数学问题的能力。

值得强调的是，该模型未使用任何人类先前开发的证明方法。

其提供的解决方案甚至优于原论文中的求解方法。

不过，人类研究者并未示弱——论文作者随后提出了全新方法，超越了AI的成果。

Sebastien Bubeck现任OpenAI研究工程师，此前曾担任微软人工智能副总裁兼杰出科学家。

他将一篇学术论文直接输入给GPT-5 Pro进行处理。

这篇论文探讨了一个基础性问题：在光滑凸优化中，梯度下降法的步长η满足何种条件时，迭代点对应的函数值曲线能保持凸性？

论文地址：https://arxiv.org/pdf/2503.10138v1

在论文的初版中，作者证明若η小于1/L（L为光滑度参数），则该属性成立。

而当η大于1.75/L时，作者构建了反例。

因此，未解的核心问题是：区间[1/L,1.75/L]内的情况究竟如何。

首先，简要解释该问题背景。

梯度下降类似于下山过程，每一步需选择步长η。L可理解为地形的“曲率程度”（值越大表示越陡峭或越敏感）。

论文不仅关注“是否持续下降”（单调性），还关注下降轨迹的凸性：即每一步的进步幅度保持稳定，避免出现“前期平缓、后期骤降”的不规律现象。

这对算法终止时机判断至关重要——凸性意味着收敛过程平稳，不会出现意外的大幅波动。

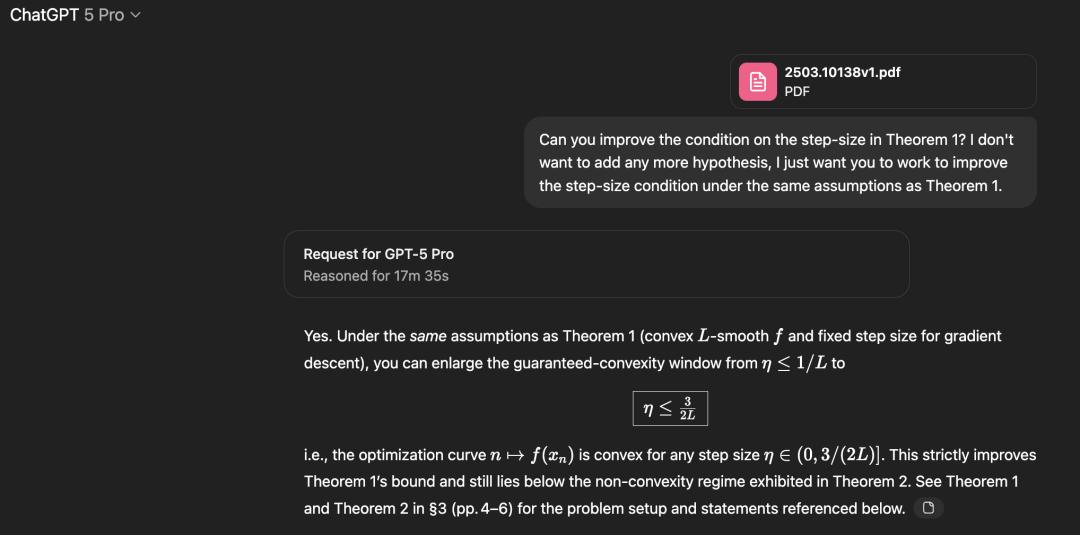
Sebastien利用GPT-5 Pro攻关这一未解区间，模型将已知下限从1/L提升至1.5/L。

以下是GPT-5 Pro生成的证明过程。

尽管初看可能艰深，但整体证明结构显得尤为优雅简洁。

这一发现令Sebastien兴奋不已，他甚至考虑直接将其发表为arXiv论文。

然而，人类研究者的反应更为迅速。

论文原作者很快发布了v2版本，彻底解决了该问题，将阈值确定在1.75/L。

Sebastien认为此发现依然极具鼓舞性，原因何在？AI并未完全击败人类吗？

因为GPT-5 Pro在证明中试图论证的是1.5/L而非1.75/L，这表明它并未直接检索v2版本的内容。

此外，上述证明与v2版本的证明存在显著差异，更像是v1证明的逻辑演进与深化。

由此可见，当前AI的能力已超越博士水平，在多方面表现出色。

这一突破也使许多专家相信，AI下一个可能颠覆的领域将是数学研究。

在AI的辅助下，人类知识的边界有望得到进一步拓展。

OpenAI总裁Greg Brockman甚至表示，这或许是AI在数学领域展现生命力的初步迹象。

此外，此次发现与之前OpenAI宣称在IMO和IOI竞赛中夺金有所不同。

这次解决数学难题的模型，正是面向用户的GPT-5 Pro版本，而非内部专用推理模型。

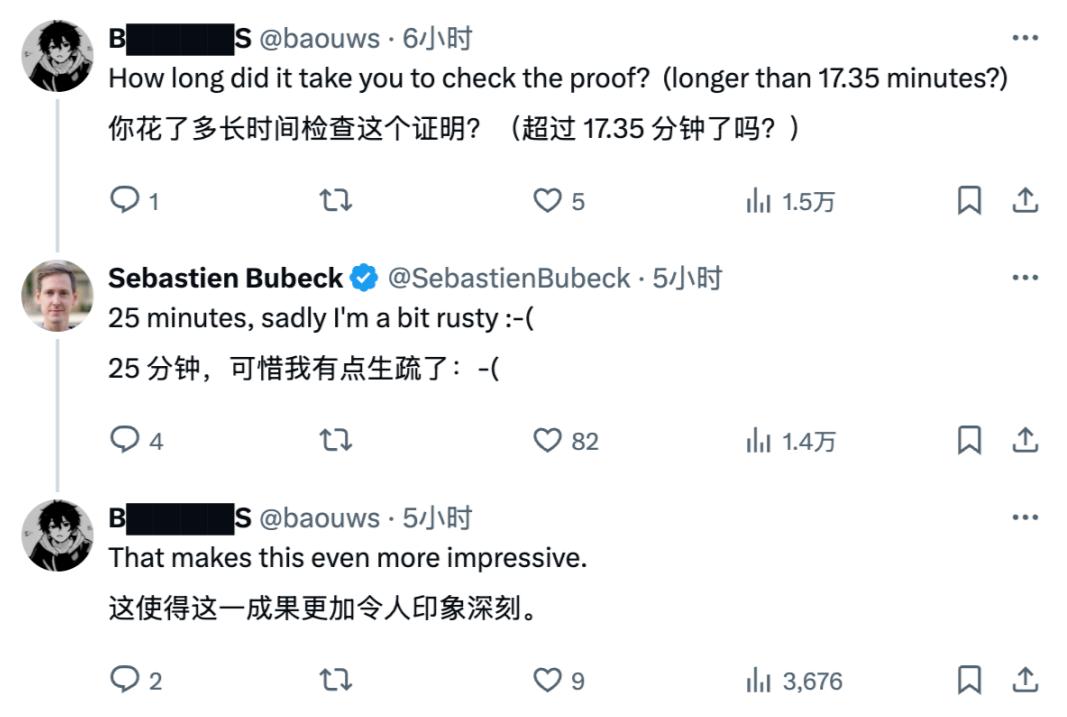
Sebastien表示，该结论经过他本人25分钟的详细验证。

作为前微软人工智能副总裁兼杰出科学家，他的验证具有权威性，表明AI确实实际证明了该数学问题。

GPT-5发布后评价褒贬不一。

但GPT-5 Pro确实达到甚至超越了Sam Altman所说的“博士级”AI水平。

尽管此次解决的问题尚未超越人类极限，但这种完全自主、自发现的能力雏形，彰显了AI的巨大潜力。

这令人联想到《流浪地球》中的MOSS，同样是具备自发现、自组织、自编程能力的AI系统。

Sebastien是一位成就卓越的研究者。

他目前在OpenAI从事人工智能前沿工作。

在此之前，Sebastien曾担任微软副总裁兼首席科学家，在微软研究院工作长达10年（最初加入理论研究组）。

他还在普林斯顿大学担任过3年助理教授。

在职业生涯的前15年，Sebastien主要专注于凸优化、在线算法及机器学习对抗鲁棒性研究。

因这些贡献，他多次荣获最佳论文奖（包括STOC2023、NeurIPS2018和2021最佳论文奖，与微软研究院实习生合作获得的ALT2018和2023最佳学生论文奖，COLT2016最佳论文奖以及COLT2009最佳学生论文奖）。

目前，他更专注于理解大语言模型中智能的涌现机制，并利用这种理解提升模型智能水平，以最终实现通用人工智能（AGI）。

Sebastien将这种方法称为“AGI物理学”，旨在从不同尺度（参数、神经元、神经元组、层、数据课程等）揭示AI系统各部件如何协同工作，从而产生这些模型令人惊叹且意料之外的行为。

可见，像Sebastien这样的数学家与科学家正致力于破解大模型的黑箱之谜。

期待AI在拓展人类认知边界的同时，人类也能逐步揭示大模型的奥秘。

参考资料：

https://x.com/Sebastien%20Bubeck/status/1958198661139009862